Régularisation des déterminants d'opérateurs - Régularisation de type Zêta

May 09, 2021

Régularisation des déterminants d'opérateurs - Régularisation de type Zêta

Le cas du Laplacien

Soit $Ω$ un domaine compact de 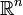$\mathbb R^n$ à bord 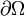$\partial \Omega$ . Sur ce domaine, on considère l'opérateur positif 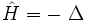$\hat{H} = - \ \Delta$ , où $Δ$ est le Laplacien, muni de conditions aux limites sur le bord 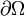$\partial \Omega$ du domaine (Dirichlet, Neumann, mixtes) qui précisent complètement le problème.

Lorsque le domaine $Ω$ est compact, l'opérateur positif 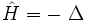$\hat{H} = - \ \Delta$ possède un spectre discret de valeurs propres auxquels est associée une base orthonormée de vecteurs propres (on utilise ici les notations de Dirac) :

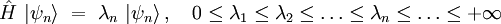
$\hat{H} \ | \psi_n \rangle \ = \ \lambda_n \ | \psi_n \rangle \, , \quad 0 \le \lambda_1 \le \lambda_2 \le \dots \le \lambda_n \le \dots \le + \infty$

Fonction zêta spectrale

On suppose ici que le fondamental 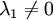$\lambda_1 \ne 0$ . Par analogie avec la fonction zêta de Riemann, on introduit la fonction zêta spectrale par la série de type Dirichlet :

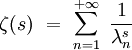
$\zeta (s) \ = \ \sum_{n=1}^{+\infty} \ \frac{1}{\lambda_n^s}$

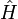Cette série ne converge que pour $\Re \mathrm{e} \left[ \, s \, \right]$ suffisamment grand, mais elle admet un prolongement méromorphe au plan entier. Lorsque le spectre de l'opérateur $\hat{H}$ n'est pas connu explicitement, on peut utiliser la définition formelle comme trace :

$\zeta (s) \ = \ \mathrm{Tr} \ \exp \ \left[ \ - \ s \ \ln \hat{H} \ \right]$

Lien avec le déterminant

Le déterminant de l'opérateur H est défini par :

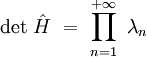
$\mathrm{det} \ \hat{H} \ = \ \prod_{n=1}^{+\infty} \ \lambda_n$

Avec l'identité :

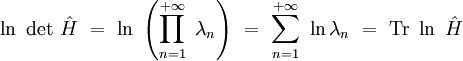
$\ln \ \mathrm{det} \ \hat{H} \ = \ \ln \ \left( \prod_{n=1}^{+\infty} \ \lambda_n \right) \ = \ \sum_{n=1}^{+\infty} \ \ln \lambda_n \ = \ \mathrm{Tr} \ \ln \ \hat{H}$

on démontre facilement la relation formelle :

$\mathrm{det} \ \hat{H} \ = \ \exp \, \left[ \, - \ \zeta'(0) \, \right]$

où la dérivée de la fonction zêta est évaluée en s = 0.

Lien avec le noyau de la chaleur

La fonction zêta est reliée par une transformée de type Mellin :

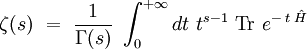
$\zeta (s) \ = \ \frac{1}{\Gamma(s)} \ \int_0^{+\infty} dt \ t^{s-1} \ \mathrm{Tr} \ e^{- \; t \; \hat{H}}$

à la trace du noyau de la chaleur, définie par :

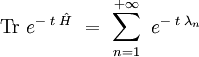
$\mathrm{Tr} \ e^{- \; t \; \hat{H}} \ = \ \sum_{n=1}^{+\infty} \ e^{- \; t \; \lambda_n}$

Lien avec Le integrale

Pour n entier, la Régularisation zêta nous permet de calculer des intégrales divergentes de la forme 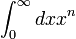$\int_{0}^{\infty}dx x^{n}$

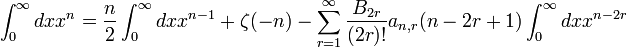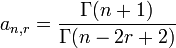$\int_{0}^{\infty}dx x^{n} = \frac{n}{2}\int_{0}^{\infty}dx x^{n-1}+ \zeta(-n) - \sum_{r=1}^{\infty}\frac{B_{2r}}{(2r)!} a_{n,r}(n-2r+1) \int_{0}^{\infty}dx x^{n-2r}$ , : $a_{n,r}= \frac{\Gamma(n+1)}{\Gamma(n-2r+2)}$ .

cette méthode a été introduite dans théorie quantique des champs par les physiciens Hartle et J. Garcia ,E. Elizalde

Extensions

Toutes les définitions précédentes se transposent assez naturellement au cas de l'opérateur de Laplace-Beltrami sur une variété riemannienne compacte, qui possède alors également un spectre discret. Elles s'étendent également au cas des variétés non-compactes à bord lorsque le spectre est encore discret

Il est également possible d'étendre la théorie pour un autre opérateur elliptique.

© Karam OUHAROU. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.

Nous sommes ravis d'améliorer notre service pour vous!

Search This Blog

M. Karam Ouharou - Siteweb officiel